Levenshtein Distance Featured

Playing with Fuzzy Logic

Playing with fuzzy logic a afternoon rabbit whole of fun experimentation. I get into some cool examples of Levenshtein distance!

Oran C

25 Sep 2023 • 6 min read

was reading the original research paper on fuzzy logic called

Fuzzy Sets by L. A. Zadeh form 1965

and wanted to see what kind of fuzzy logic member functions look like.

soooo....

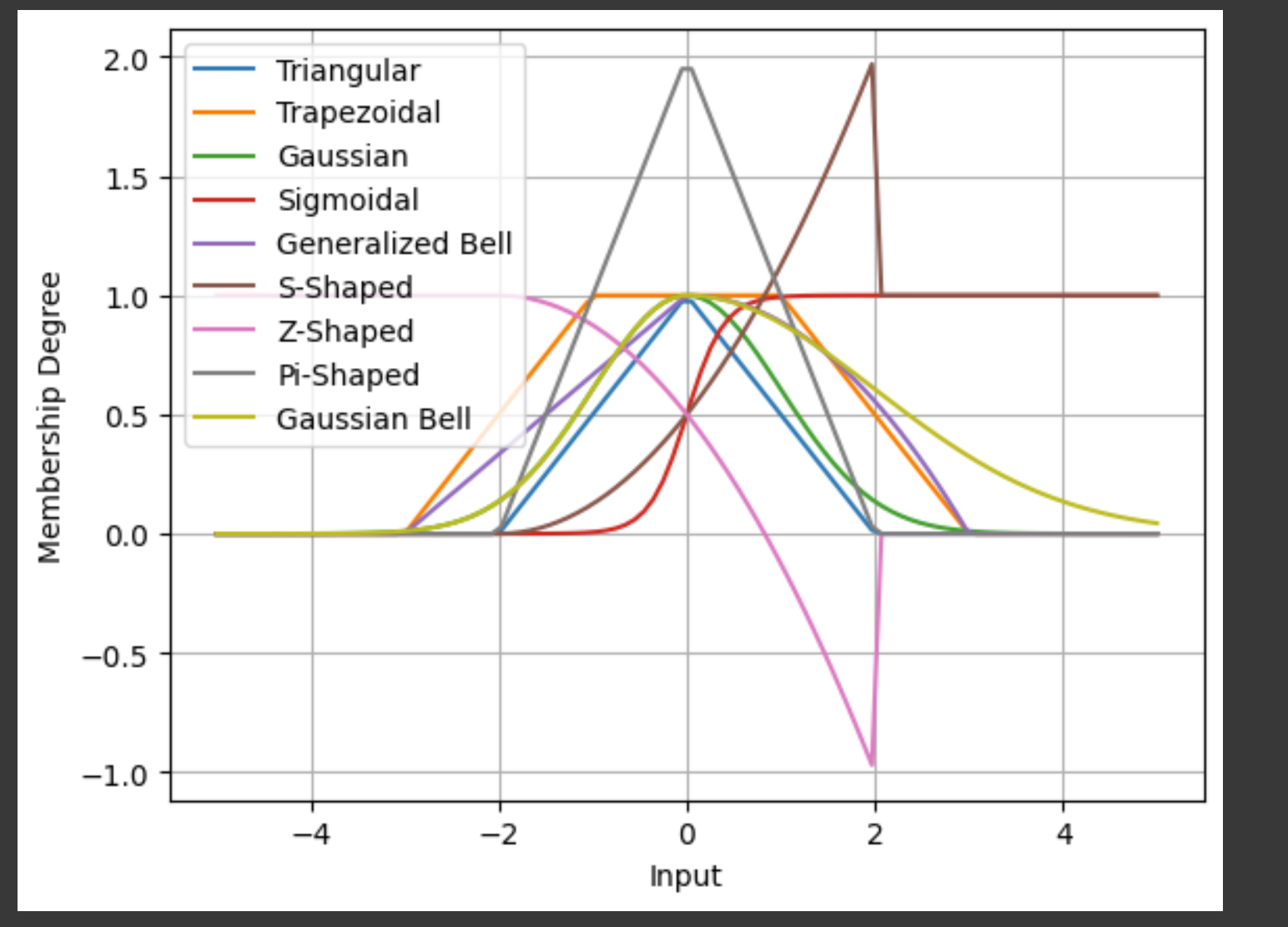
the output was quite pretty

and make me realize all it is a function that defines wither an objects is considered part of a class or not. and uses 0 to 1 to determin wither its inside the set or not

lets look at a simple example (well kindof simple)

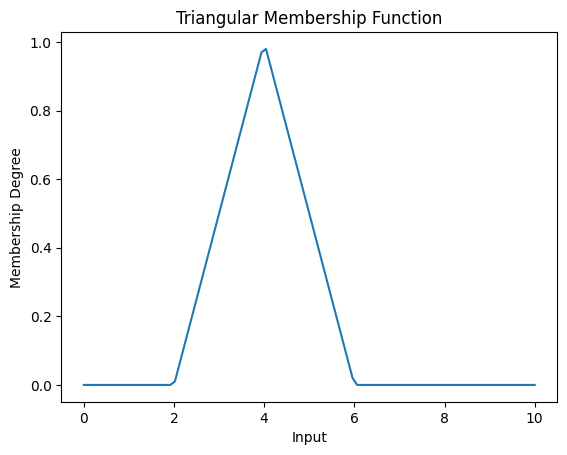
def triangular(x, a, b, c):
    if a <= x <= b:
        return (x - a) / (b - a)
    elif b < x <= c:
        return (c - x) / (c - b)
    else:
        return 0

AI explains as follows source: claud.ai

This Python function calculates the triangular membership function value for an input x given parameters a, b, and c.

The triangular membership function is often used in fuzzy logic systems. It takes on a triangular shape between 3 points a, b, and c.

Here's how it works:

It first checks if x is between a and b. If so, it calculates the slope of the line between (a, 0) and (b, 1) to determine the output value.
Next it checks if x is between b and c. If so, it calculates the slope of the line between (b, 1) and (c, 0) to determine the output value.
If x is less than a or greater than c, it returns 0.
So the function returns the "degree of membership" between 0 and 1 for the input x, based on a triangular fuzzy set defined by the three points a, b and c.

The slope calculations essentially map the input x onto the ascending and descending sides of the triangle. This allows fuzzy logic systems to map inputs to fuzzy categories and determine a degree of membership.

what the f does all this mean? and why a tryangle?

well the real world is non-binary

when you encounter real world data its often living on a continium where its kinda a 'animial', kinda a 'plant'.

this allows for gradual inclusion and exclusion to the set.

machine learning uses this to grate effect

and example 'member' function so to speak (ml people call it a activation funciton if you want to be pedantic)
ReLu (Rectified Linear Unit) Membership Function

and Crowd favorite

Spline

if your interested in splines you have to check out Freya Holm its 1 hour long, but omg! its amazing

heres all the functions in one graph

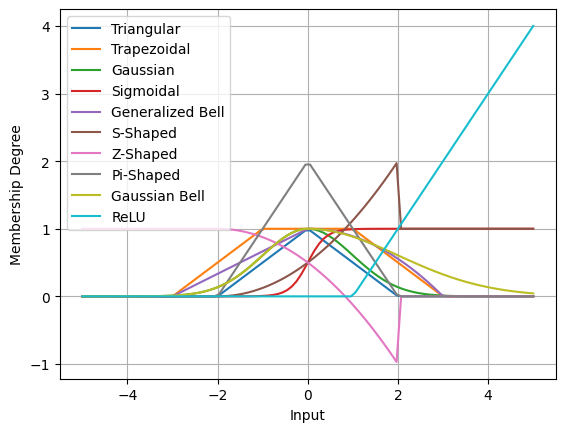
Why care?

well fuzzy logic is are really useful!

example you want to search a book for some keyword but dont have the spelling just write, for example you look for an 🍎, but spelled it incorrectly 'appel'

lets do some string search using `Levenshtein` distance

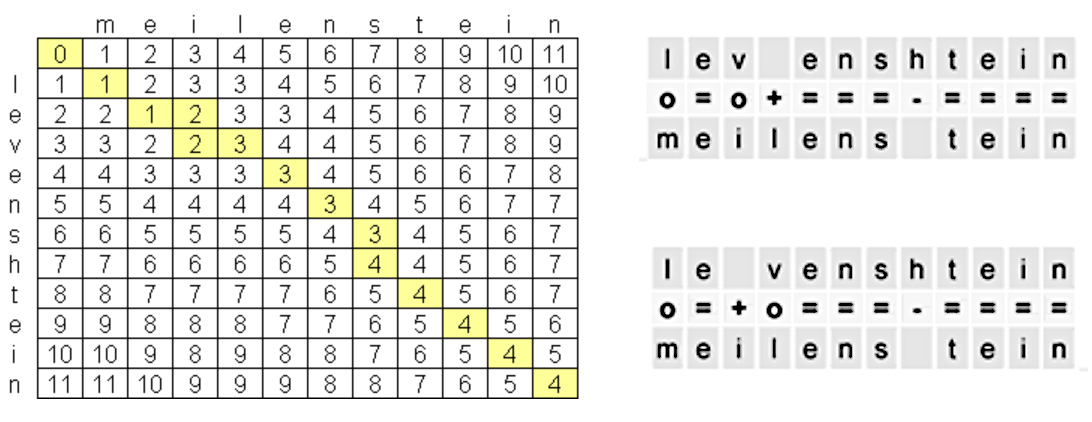
source Levenshtein Distance

What this does is checks the similarity between to strings

lets use fuzzy logic to create a set of appl like things

here we write some code that checks to see what words are closest match to out input word "appel"

this is the triangle fuzzy member function

def levenshtein_similarity(word1, word2, max_distance):
    distance = Levenshtein.distance(word1, word2)
    //triangle member function part
    membership_degree = 1 - (distance / max_distance)
    return max(0, min(1, membership_degree))

our word list

word_list = [
	"apple", "banana", "cherry", "date", "elderberry", "fig", "grape", "kiwi","appliance","appliances","applicable","applicant","applicants","application","applications","applied","applies","apply","applying","appointed","appointment","appointments","appraisal","appreciate","appreciated","appreciation","approach","approaches","appropriate","appropriations","approval","approve","approved","approx","approximate","approximately"
]

heres the output

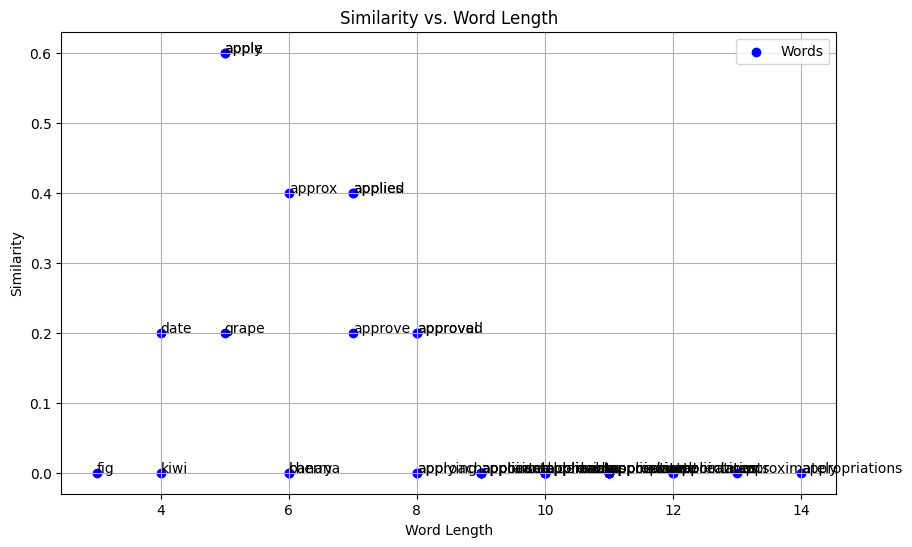
this graph shows that approx, and applied are most similar to appel

heres the fuzzy set it creates

heres the full code if your interested

#!pip install python-Levenshtein

import matplotlib.pyplot as plt
import numpy as np
import Levenshtein
# Function to calculate Levenshtein similarity
def levenshtein_similarity(word1, word2, max_distance):
    distance = Levenshtein.distance(word1, word2)
    membership_degree = 1 - (distance / max_distance)
    return max(0, min(1, membership_degree))

# List of words
word_list = ["apple", "banana", "cherry", "date", "elderberry", "fig", "grape", "kiwi", "appliance","appliances","applicable","applicant","applicants","application","applications","applied","applies","apply","applying","appointed","appointment","appointments","appraisal","appreciate","appreciated","appreciation","approach","approaches","appropriate","appropriations","approval","approve","approved","approx","approximate","approximately"]
# Target word for similarity search
target_word = "appel"  # Intentional typo to demonstrate Levenshtein similarity

# Calculate Levenshtein similarity
similar_words = []
similarity_threshold = 0.3  # Adjust this threshold as needed

for word in word_list:
    similarity = levenshtein_similarity(target_word, word, max_distance=len(target_word))
    if similarity > similarity_threshold:
        similar_words.append((word, similarity))

# Create a fuzzy set with membership values above the threshold
fuzzy_set = []
for word, similarity in similar_words:
    fuzzy_set.append((word, triangular(similarity, 0, 1, 0.3)))

# Print the fuzzy set
print("Fuzzy Set:")
for word, membership in fuzzy_set:
    print(f"{word}: {membership:.2f}")

# Create a scatter plot
plt.figure(figsize=(10, 6))
for word, membership in fuzzy_set:
    plt.scatter([len(word)], [membership], c='b', marker='o', label='Words')

# Add labels and title
plt.xlabel('Word Length')
plt.ylabel('Membership Degree')
plt.title('Fuzzy Set: Membership vs. Word Length')

# Annotate the points with word labels
for word, membership in fuzzy_set:
    plt.annotate(word, (len(word), membership))

# Show the plot
plt.grid(True)
plt.legend()
plt.show()


# Calculate Levenshtein similarity and word lengths
similarities = []
word_lengths = []

for word in word_list:
    similarity = levenshtein_similarity(target_word, word, max_distance=len(target_word))
    word_length = len(word)
    similarities.append(similarity)
    word_lengths.append(word_length)

# Create a scatter plot
plt.figure(figsize=(10, 6))
plt.scatter(word_lengths, similarities, c='b', marker='o', label='Words')

# Add labels and title
plt.xlabel('Word Length')
plt.ylabel('Similarity')
plt.title('Similarity vs. Word Length')

# Annotate the points with word labels
for i, word in enumerate(word_list):
    plt.annotate(word, (word_lengths[i], similarities[i]))

# Show the plot
plt.grid(True)
plt.legend()
plt.show()